ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 9 стр. 88
Условие
Докажите, что каждая сторона треугольника меньше суммы двух других сторон. Что такое неравенство треугольника?
Решение #1
Теорема:
Каждая сторона треугольника меньше суммы двух других сторон.
Доказательство:
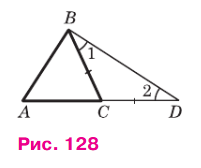
Рассмотрим произвольный треугольник ABC и докажем, что AB < АС + СВ. Отложим на продолжении стороны АС отрезок CD, равный стороне СВ (рис. 128). В равнобедренном треугольнике BCD ∠1 = ∠2, а в треугольнике ABD ∠ABD > ∠1 и, значит, ∠ABD > ∠2. Так как в треугольнике против большего угла лежит большая сторона, то AB < AD. Но AD = AC + CD = AC + CB, поэтому AB < АС + СВ.
Сообщить об ошибке
Сообщитe об ошибке