ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 8 стр. 159
Условие
Какой отрезок называется средней линией треугольника? Сформулируйте и докажите теорему о средней линии треугольника.
Решение #1
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой сто роны.
Доказательство:
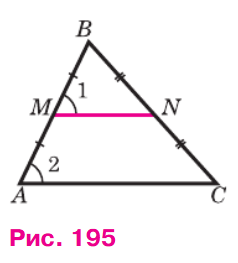
Пусть MN — средняя линия треугольника ABC (рис. 195). Докажем, что MN || AC и MN=1/2AC.
Треугольники BMN и ВАС подобны по второму признаку подобия треугольников (∠B — общий, BM/BA=BN/BC=1/2), поэтому ∠1 = ∠2 и MN/AC=1/2. Из равенства ∠1 = ∠2 следует, что MN || AC (объ-ясните почему), а из второго равенства — что MN=1/2AC. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке