ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 729 стр. 187

1. Пусть в четырехугольнике ABCD выполняется условие:

∠A+∠C=180∘.(1)

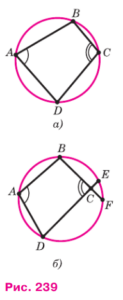
2. Рассмотрим окружность, проходящую через три вершины четырехугольника A, B и D (см. рис. 239, а). Необходимо доказать, что эта окружность также проходит через вершину C.

3. Предположим, что точка C не лежит на этой окружности. Тогда она может находиться либо внутри круга, либо вне его.

Случай 1: точка C внутри круга

4. Если точка C находится внутри окружности, то по свойству углов, опирающихся на одну и ту же дугу, имеем:

∠C=1/2 ​(U DAB+U EFD),

где E и F — точки касания с окружностью.

5. Следовательно,

∠C>1/2 U DAB.

6. Так как

∠A=1/2 U BED,

то можно записать:

∠A+∠C>1/2​(U BED+U DAB).

7. Это приводит к тому, что

∠A+∠C>90∘+90∘=180∘.

8. Однако это противоречит условию (1):

∠A+∠C=180∘.

Случай 2: точка C вне круга

9. Аналогично можно рассмотреть случай, когда точка C находится вне круга. В этом случае также можно показать, что сумма углов будет больше 180∘, что снова приведет к противоречию с условием (1).

Таким образом, наше предположение о том, что точка C не лежит на окружности неверно. Следовательно, точка C должна лежать на описанной окружности.