ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 724 стр. 186
Пусть в выпуклом четырехугольнике выполняется условие:
Докажем, что в четырехугольник можно вписать окружность.
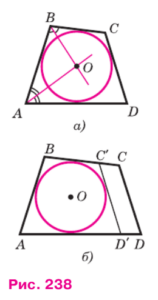
1. Рассмотрим точку , которая является точкой пересечения биссектрис углов и . Эта точка равноудалена от сторон , и . Следовательно, можно провести окружность с центром в точке , касающуюся этих трех сторон (см. рис. 238, а).
2. Нам нужно доказать, что эта окружность также касается стороны . Предположим, что это не так. Тогда прямая либо не имеет общих точек с окружностью, либо является секущей.
3. Случай 1:
Прямая CD не имеет общих точек с окружностью. В этом случае проведем касательную к окружности из точки , которая будет параллельна стороне (обозначим точки пересечения касательной со сторонами и как и ).
4. Четырехугольник будет описанным, так как его стороны касаются окружности. По свойству описанных четырехугольников имеем:
5. Учитывая, что длины отрезков равны:
6. Подставляя эти выражения в (2), получаем:
Перепишем это уравнение как:
7. Поскольку по условию (1) у нас есть равенство
то правая часть этого равенства равна :
8. Мы получили равенство
что означает, что в четырехугольнике одна сторона равна сумме трех других сторон, что невозможно.
9. Случай 2:
Аналогично можно рассмотреть случай, когда прямая является секущей для окружности. В этом случае также придем к противоречию.
Таким образом, мы приходим к выводу, что предположение о том, что сторона не касается окружности или является секущей, неверно. Следовательно, окружность действительно касается стороны .