ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 642 стр. 166
Условие
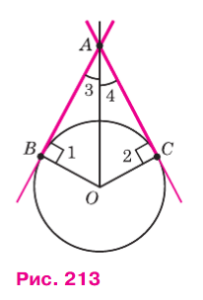
На рисунке 213 ОВ = 3 см, ОА = 6 см. Найдите AB, AC, ∠3 и ∠4.
Решение #1
1. Треугольник AOB — прямоугольный (так как AB — касательная к окружности в точке B, а OB — радиус). По теореме Пифагора:
AB² = OA² — OB² = 6² — 3² = 36 — 9 = 27
AB = √27 = 3√3 см
2. Треугольник AOC также прямоугольный (AC — касательная, OC — радиус). Поскольку OA, OB и OC одинаковы (OA — общая гипотенуза, OB = OC = радиус), треугольники AOB и AOC равны (по гипотенузе и катету). Поэтому:
AC = AB = 3√3 см
3. В прямоугольном треугольнике AOB:
sin(∠3) = OB / OA = 3 / 6 = 1/2
∠3 = arcsin(1/2) = 30°
4. Так как треугольники AOB и AOC равны, ∠3 = ∠4 = 30°
Сообщить об ошибке
Сообщитe об ошибке