ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 600 стр. 158
Условие
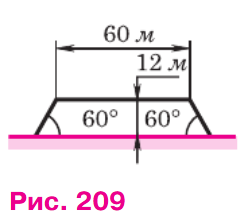
Насыпь шоссейной дороги имеет в верхней части ширину 60 м. Какова ширина насыпи в нижней её части, если угол наклона откосов равен 60°, а высота насыпи равна 12 м (рис. 209)?
Решение #1
Обозначим ширину нижней части насыпи через x. Поскольку угол наклона откосов равен 60°, а высота насыпи равна 12 м, мы можем использовать тригонометрические функции для нахождения ширины нижней части.
Рассмотрим прямоугольный треугольник, образованный высотой насыпи (12 м), половиной разницы между верхней и нижней шириной насыпи (1/2 * (x — 60) м), и частью откоса. В этом треугольнике, тангенс угла 60° равен отношению противолежащего катета (высота насыпи) к прилежащему катету (половина разницы ширин).
tg 60° = 12 / ((x — 60) / 2)
tg 60° = √3
√3 = 24 / (x — 60)
(x — 60) = 24 / √3
(x — 60) ≈ 13,86
x ≈ 60 + 13,86
x ≈ 74 м
Сообщить об ошибке
Сообщитe об ошибке