ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 6 стр. 158
Условие
Сформулируйте и докажите теорему, выражающую второй признак подобия треугольников.
Решение #1
Теорема:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие тре угольники подобны.
Доказательство:
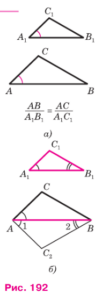
Рассмотрим два треугольника ABC и А1В1С1, у которых AB/A1B1=AC/A1C1, ∠A = ∠A1 (рис. 192, а). Докажем, что ΔABС и ΔA1B1C1 подобны. Для этого, учитывая первый признак подобия тре угольников, достаточно доказать, что ∠B = ∠B1.
Рассмотрим треугольник ABС2, у которого ∠1 = ∠A1, ∠2 = ∠B1 (рис. 192, б). Треугольники ABС2 и A1B1С1 подобны по первому признаку по-добия треугольников, поэтому AB/A1B1=AC2/A1C1. С другой стороны, по условию AB/A1B1=AC/A1C1. Из этих двух равенств получаем АС = АС2.
Треугольники ABC и ABС2 равны по двум сторонам и углу между ними (AB — общая сторона, АС = АС2 и ∠A = ∠1, поскольку ∠A = ∠A1 и ∠1 = ∠A1). Отсюда следует, что ∠B = ∠2, а так как ∠2 = ∠B1, то ∠B = ∠B1. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке