ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 556 стр. 144

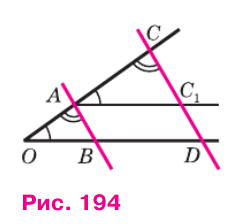
1. Проведем через точку A прямую AC₁ параллельно BD. Эта прямая пересекает прямую CD в точке C₁.

2. Рассмотрим треугольники ΔOAB и ΔACC₁. У них есть:

∠OAB = ∠ACC₁: это соответственные углы при параллельных прямых AB и C₁C, пересеченных секущей OC.

∠AOB = ∠AC₁C: это вертикальные углы.

Таким образом, треугольники ΔOAB и ΔACC₁ подобны по двум равным углам (по признаку подобия треугольников). Из подобия следует:

OA/AC₁ = OB/CC₁

3. Четырехугольник AC₁DB — параллелограмм, поскольку AC₁ || BD (по построению) и AB || C₁D (данное условие). В параллелограмме противоположные стороны равны, следовательно:

AC₁ = BD

4. Подставим AC₁ = BD в соотношение из подобия треугольников:

OA/BD = OB/CC₁

Перекрестное умножение дает:

OA * CC₁ = OB * BD

Из рисунка видно, что CC₁ = AC. Поэтому

OA * AC = OB * BD

Разделив обе части уравнения на OB * AC, получаем:

OA/OB = AC/BD

Что и требовалось доказать.