ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 5 стр. 158
Условие
Сформулируйте и докажите теорему, выражающую первый признак подобия треугольников.
Решение #1
Теорема:
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Доказательство:
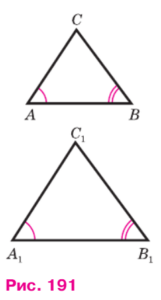
Пусть ΔABС и ΔA1B1C1 — два треугольника, у которых ∠A = ∠A1, ∠B = ∠B1 (рис. 191). Докажем, что ΔABC и ΔA1B1C1 подобны.
По теореме о сумме углов треугольника ∠C = 180° − ∠A − ∠B, ∠C1 = 180° − ∠A1 − ∠B1, и, значит, ∠C = ∠C1. Таким образом, углы треугольника ABC соответственно равны углам треугольника А1В1С1.
Докажем, что стороны треугольника ABC пропорциональны сходственным сторонам треугольника А1В1С1. Так как ∠A = ∠A1 и ∠C = ∠C1, то SABC/SA1B1C1 = AB*AC/A1B1*A1C1 и SABC/SA1B1C1 = CA*CB/C1A1*C1B1 (см. п. 53).
Из этих равенств следует, что AB/A1B1=BC/B1C1. Аналогично, используя равенства ∠A = ∠A1, ∠В = ∠В1, получаем BC/B1C1=CA/C1A1. Итак, стороны треугольника ABC пропорциональны сходственным сторонам треугольника А1В1С1. Теорема доказана.
Сообщить об ошибке
Сообщитe об ошибке