ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 298 стр. 89

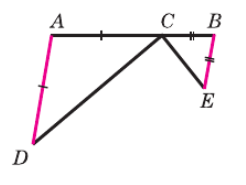
1. Поскольку AC = AD (дано), треугольник ADC является равнобедренным.

Следовательно, углы при основании равны: ∠D = ∠ACD (или ∠CDA = ∠DCA).

Поскольку BC = BE (дано), треугольник BCE является равнобедренным.

Следовательно, углы при основании равны: ∠E = ∠BCE (или ∠CEB = ∠CEB).

2. В треугольнике ADC: ∠DAC + ∠D + ∠ACD = 180°.

В треугольнике BCE: ∠CBE + ∠E + ∠BCE = 180°.

3. Так как AD || BE (дано), а прямая AB является секущей, сумма односторонних внутренних углов равна 180°.

Следовательно, ∠DAB + ∠ABE = 180°.

Здесь ∠DAB — это то же самое, что ∠DAC или просто ∠A в контексте ∆ADC.

А ∠ABE — это то же самое, что ∠CBE или просто ∠B в контексте ∆BCE).

То есть, ∠A + ∠B = 180°.

4. Выразим углы A и B через другие углы треугольников:

Из суммы углов в ∆ADC: ∠A = 180° — (∠D + ∠ACD).

Из суммы углов в ∆BCE: ∠B = 180° — (∠E + ∠BCE).

5. Подставим выражения для углов A и B в равенство из п.3:

(180° — (∠D + ∠ACD)) + (180° — (∠E + ∠BCE)) = 180°

360° — (∠D + ∠ACD + ∠E + ∠BCE) = 180°

-(∠D + ∠ACD + ∠E + ∠BCE) = 180° — 360°

-(∠D + ∠ACD + ∠E + ∠BCE) = -180°

∠D + ∠ACD + ∠E + ∠BCE = 180°.

6. Используем равенство углов из п.1:

Поскольку ∠D = ∠ACD и ∠E = ∠BCE, подставим это в последнее равенство:

∠ACD + ∠ACD + ∠BCE + ∠BCE = 180°

2 * ∠ACD + 2 * ∠BCE = 180°

2 * (∠ACD + ∠BCE) = 180°

∠ACD + ∠BCE = 90°.

7. Углы на прямой:

Точки A, C, B лежат на одной прямой, следовательно, угол ∠ACB является развернутым и равен 180°.

Угол ∠ACB состоит из трех углов: ∠ACD, ∠DCE и ∠BCE.

Таким образом, ∠ACD + ∠DCE + ∠BCE = 180°.

8. Найдем угол DCE:

Из п.6 мы знаем, что ∠ACD + ∠BCE = 90°.

Подставим это в равенство из п.7:

90° + ∠DCE = 180°

∠DCE = 180° — 90°

∠DCE = 90°.

Таким образом, угол DCE — прямой, что и требовалось доказать.