ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 246 стр. 74

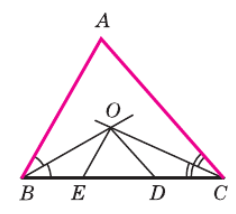
1. Нам дано, что OE || AB.

Прямая BO является секущей, пересекающей эти две параллельные прямые (OE и AB).

При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.

Следовательно, ∠ABO = ∠BOE (эти углы являются накрест лежащими).

2. BO — биссектриса угла ABC. Это означает, что ∠ABO = ∠OBC (биссектриса делит угол на две равные части).

Из Шага 1 мы знаем, что ∠ABO = ∠BOE. Из определения биссектрисы мы знаем, что ∠ABO = ∠OBC. Из этих двух равенств следует, что ∠OBC = ∠BOE.

Если в треугольнике два угла равны, то этот треугольник является равнобедренным, и стороны, лежащие против этих равных углов, тоже равны.

В треугольнике BOE, мы только что показали, что ∠OBC (который можно также обозначить как ∠OBE, так как точка E лежит на BC) равен ∠BOE.

Против угла ∠OBC лежит сторона OE. Против угла ∠BOE лежит сторона BE.

Поскольку ∠OBC = ∠BOE, треугольник BOE является равнобедренным, и, следовательно, BE = EO.

3. Нам дано, что OD || AC.

Прямая CO является секущей, пересекающей эти две параллельные прямые (OD и AC).

При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.

Следовательно, ∠ACO = ∠DOC (эти углы являются накрест лежащими).

4. CO — биссектриса угла BCA. Это означает, что ∠ACO = ∠OCD (биссектриса делит угол на две равные части).

Из Шага 3 мы знаем, что ∠ACO = ∠DOC.

Из определения биссектрисы мы знаем, что ∠ACO = ∠OCD.

Из этих двух равенств следует, что ∠OCD = ∠DOC.

Если в треугольнике два угла равны, то этот треугольник является равнобедренным, и стороны, лежащие против этих равных углов, тоже равны.

В треугольнике DOC, мы только что показали, что ∠OCD равен ∠DOC.

Против угла ∠OCD лежит сторона OD.

Против угла ∠DOC лежит сторона DC.

Поскольку ∠OCD = ∠DOC, треугольник DOC является равнобедренным, и, следовательно, OD = DC.

5. Периметр треугольника EDO (P_EDO) — это сумма длин его сторон:

P_EDO = OE + OD + ED.

Из рисунка видно, что отрезок BC состоит из трех отрезков: BE, ED и DC.

BC = BE + ED + DC.

Теперь используем равенства, которые мы доказали в Шаге 2 (BE = EO) и Шаге 4 (OD = DC).

Подставим эти равенства в выражение для BC:

BC = (EO) + ED + (OD).

Сравнивая полученное выражение для BC с выражением для периметра P_EDO:

P_EDO = OE + OD + ED

BC = OE + OD + ED

Очевидно, что P_EDO = BC.

Что и требовалось доказать.