ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 22 стр. 185
Условие
Сформулируйте и докажите теорему об окружности, вписанной в треугольник. Сколько окружностей можно вписать в данный треугольник?
Решение #1
Теорема:
В любой треугольник можно вписать окружность.
Доказательство:
Рассмотрим произвольный треугольник ABC и обозначим буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры OK, OL и OM соответственно к сторонам AB, ВС и СА (см. рис. 232). Так как точка О равноудалена от сторон треугольника ABC, то OK = OL = OM. Поэтому окружность с центром О радиуса ОK проходит через точки K, L и М. Стороны треугольника ABC касаются этой окружности в точках K, L, M, так как они перпендикулярны к радиусам ОK, OL и OM. Значит, окружность с центром О радиуса ОK является вписанной в треугольник ABC. Теорема доказана.
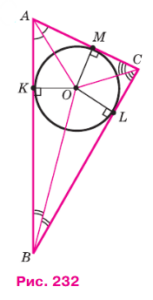
Отметим, что в треугольник можно вписать только одну окружность.
Сообщить об ошибке
Сообщитe об ошибке