ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 216 стр. 67

Дополнительные обозначения:

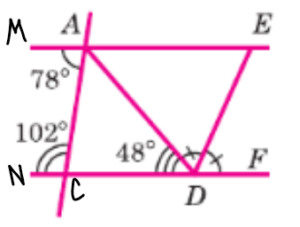
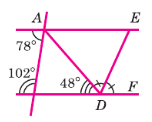
1. Определяем, являются ли прямые AE и DF параллельными.

Угол MAC = 78° и угол NCA = 102°. Эти углы расположены между прямыми AE и DF, по одну сторону от секущей AC. Они называются односторонними внутренними углами.

Если сумма односторонних внутренних углов, образованных двумя прямыми и секущей, равна 180°, то эти прямые параллельны.

Проверка: 78° + 102° = 180°.

Поскольку сумма односторонних внутренних углов равна 180°, прямые AE параллельна DF (AE || DF). Это ключевой момент.

2. Находим величину угла DAE (или EAD).

Мы только что доказали, что AE || DF. Прямая AD является секущей, пересекающей эти две параллельные прямые.

Углы ∠DAE и ∠ADF являются накрест лежащими углами относительно параллельных прямых AE и DF и секущей AD. Накрест лежащие углы равны.

Угол ∠ADF на рисунке четко обозначен как 48°.

Так как AE || DF, то ∠DAE = ∠ADF.

Следовательно, ∠DAE = 48°.

Первый угол треугольника ADE равен ∠DAE = 48°.

3. Находим величину угла ADE.

Поскольку угол ADE=углу FDE (поскольку DE — биссектриса), а также имеется развёрнутый угол NDF=180°, мы можем найти с помощью уравнения, где x=угол ADE=угол FDE

x+x+ADN=180°

2x+48°=180°

2x=180°-48°

2x=132°

x=66°

Значит, второй угол треугольника ADE равен ∠ADE = 66°.

4. Находим величину угла DEA (или AED).

Сумма всех углов в любом треугольнике всегда равна 180°.

Для треугольника ADE: ∠DAE + ∠ADE + ∠DEA = 180°

Подставляем найденные значения: 48° + 66° + ∠DEA = 180°

Складываем известные углы: 114° + ∠DEA = 180°

Вычисляем ∠DEA: ∠DEA = 180° — 72° = 66°.

Третий угол треугольника ADE равен ∠DEA = 66°.