ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 18 стр. 89
Условие
Докажите, что все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Решение #1
Рассмотрим параллельные прямые а и b. Отметим на прямой а точку А и проведём из этой
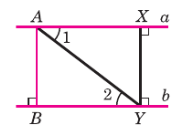
точки перпендикуляр AB к прямой b (рис. 138). Докажем, что расстояние от любой точки X прямой а до прямой b равно AB.
Проведём из точки X перпендикуляр XY к прямой b. Так как ХY ⊥ b, то XY ⊥ a. Прямоугольные треугольники ABY и YХА равны по гипотенузе и острому углу (AY — общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых а и b секущей АY). Следовательно, ХY = AB.
Итак, любая точка X прямой а находится на расстоянии AB от прямой b. Очевидно, все точки прямой b находятся на таком же расстоянии от прямой а.
Сообщить об ошибке
Сообщитe об ошибке