ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 16 стр. 114
Условие
Какой четырёхугольник называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Решение #1
Ромбом называется параллелограмм, у которого все стороны равны.
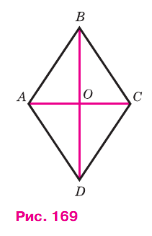
Рассмотрим ромб ABCD (рис. 169). Требуется доказать, что его диагонали AC и BD взаимно перпендикулярны и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ∠BAC = ∠DAC.
По определению ромба все его стороны равны, в частности AB = AD, поэтому треугольник BAD равнобедренный. Так как ромб является параллелограммом, то его диагонали точкой О пересечения делятся пополам. Следовательно, отрезок АО — медиана равнобедренного треугольника BAD, проведённая к основанию, а значит, высота и биссектриса этого тре угольника. Поэтому AC ⊥ BD и ∠BAC = ∠DAC, что и требовалось доказать.
Сообщить об ошибке
Сообщитe об ошибке