ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 13 стр. 159

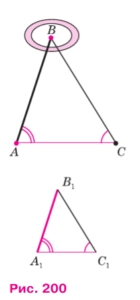
Предположим, что нам нужно определить высоту какого-нибудь предмета, например высоту телеграфного столба А1С1, изображённого на рисунке 199. Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А1 столба, как показано на рисунке. Отметим на поверхности земли точку В, в которой прямая A1A пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников (∠C1 = ∠C = 90°, ∠B — общий). Из подобия треугольников следует: A1C1/AC=BC1/BC, откуда

A1C1=(AC*BC1)/BC.

Измерив расстояния ВС1 и ВС и зная длину АС шеста, по полученной формуле определяем высоту А1С1 телеграфного столба. Если, например, ВС1 = 6,3 м, ВС = 2,1 м, АС = 1,7 м, то A1C1=(1,7*6,3)/2,1=5,1 м.

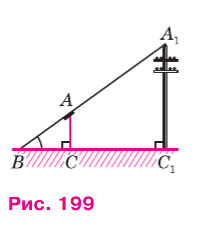
Затем с помощью астролябии измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник A1B1C1, у которого ∠A1 = ∠A, ∠C1 = ∠C, и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольники ABC и А1В1С1 подобны (по первому признаку подобия треугольников), то AB/A1B1=AC/A1C1, откуда получаем AB=(AC*A1B1)/A1C1. Эта формула позволяет по известным расстояниям АС, A1C1 и А1В1 найти расстояние AB.

Для упрощения вычислений удобно построить треугольник А1В1С1 таким образом, чтобы A1C1 : AC = 1 : 1000. Например, если АС = 130 м, то расстояние А1C1 возьмём равным 130 мм. В этом случае AB = AC/A1C1 ⋅ А1В1 = 1000 ⋅ А1B1, поэтому, измерив расстояние А1В1 в миллиметрах, мы сразу получим расстояние AB в метрах.