ГДЗ по геометрии 7 класс В. Ф. Бутузов, И. И. Юдина, Л. С. Атанасян, С. Б. Кадомцев, Э. Г. Позняк упражнение - 10 стр. 159
Условие
Сформулируйте и докажите утверждение о том, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники.
Решение #1
Утверждение:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Доказательство:
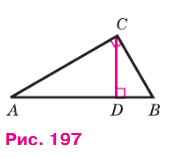
Пусть ΔABC — прямоугольный треугольник с прямым углом С, CD — высота, проведённая из вершины С к гипотенузе AB (рис. 197). Докажем, что ΔABC подобен ΔACD, ΔABC подобен ΔCBD, ΔACD подобен ΔCBD.
Треугольники ABC и ACD подобны по первому признаку подобия треугольников (∠A — общий, ∠ACB = ∠ADC = 90°). Точно так же подобны треугольники ABC и CBD (∠B — общий и ∠ACB = ∠BDC = 90°), поэтому ∠A = ∠BCD. Наконец, треугольники ACD и CBD также подобны по первому признаку подобия (в этих треугольниках углы с вершиной D прямые и ∠A = ∠BCD), что и требовалось доказать.
Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков AB и CD, если
XY=√(AB*CD).
Сообщить об ошибке
Сообщитe об ошибке