Главная/ 10 класс/ Физика/ Рымкевич А.П. Физика 10-11 класс. Задачник/ 84 стр. 18

ГДЗ по физике 10 класс Рымкевич А.П. упражнение - 84 стр. 18

1...818283...375

84 стр. 18

Условие

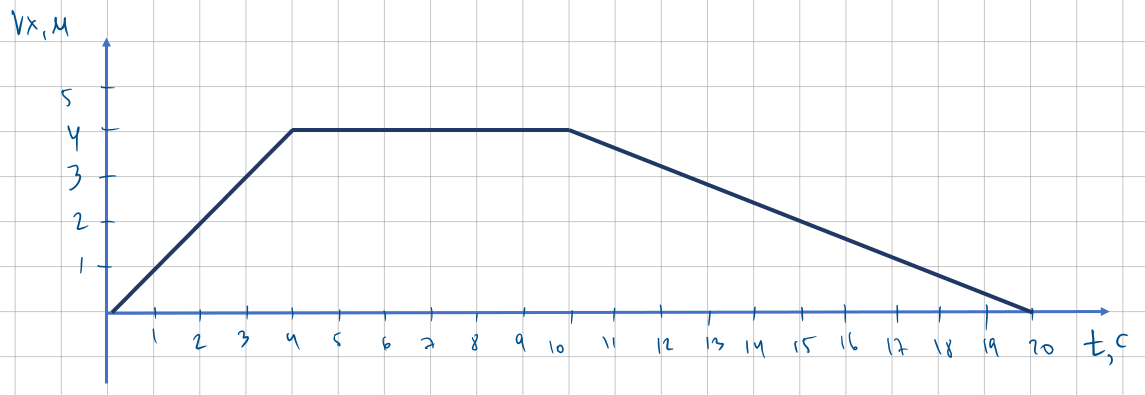
Велосипедист начал свое движение из состояния покоя и в течение первых $4 с$ двигался с ускорением $1 м / с^{2}$ ; затем в течение $0, 1 мин$ он двигался равномерно и последние $20 м$ — равнозамедленно до остановки. Найти среднюю скорость за все время движения. Построить график зависимости $υ_{x} (t)$ .

Решение #1

Длина первого участка пути велосипедиста: $S_{1} = υ_{01} t_{1} + \frac{a_{1} t_{1}^{2}}{2} = \frac{a_{1} t_{1}^{2}}{2} = \frac{1 \cdot 4^{2}}{2} = 8 м$

Его скорость в конце первого участка: $υ_{1} = υ_{01} + a_{1} t_{1} = a_{1} t_{1} = 1 \cdot 4 = 4 м / с$

Скорость на участке 1: $υ_{1} = υ_{01} + a_{1} t = a_{1} t = t$

Длина второго участка пути: $S_{2} = υ_{1} t_{2} = 4 \cdot 6 = 24 м$

Скорость на участке 2: $υ_{2} = υ_{1} + a_{2} t = υ_{1} = 4$

Скорость, путь и ускорение на третьем участе пути:

$0 = υ 1 + a_{3} t_{3} \Rightarrow t_{3} = — \frac{υ_{1}}{a_{3}}$

$S_{3} = υ_{1} t_{3} + \frac{a_{3} t_{3}^{2}}{2} = — \frac{υ_{1}^{2}}{a_{3}} + \frac{a_{3} υ_{1}^{2}}{2 a_{3}^{2}} = — \frac{υ_{1}^{2}}{2 a_{3}}$

$a_{3} = — \frac{υ_{1}^{2}}{2 S_{3}} = — \frac{4^{2}}{2 \cdot 20} = — 0, 4 м / с^{2}$

$t_{3} = — \frac{4}{— 0, 4} = 10 с$

Скорость на участке 3: $υ_{3} = υ_{2} + a_{3} t = 4 — 0, 4 t$

Средняя скорость на всем пути:

$υ_{с р} = \frac{S_{1} + S_{2} + S_{3}}{t_{1} + t_{2} + t_{3}} = \frac{8 + 24 + 20}{4 + 6 + 10} = 2, 6 м / с$

Сообщить об ошибке

1...818283...375